[Image above] Frameworks that correlate various aspects of a ceramic’s structure with its properties improve researchers’ ability to design new and improved materials. Credit: PxHere
During my school years, I usually jumped on the chance to gain extra credit by doing additional homework problems. But when our physics professor offered credit to anyone who could solve a certain physics problem while accounting for air resistance, I gladly stood that one out. There’s a reason why physicists typically ignore air resistance—it took my peers hours to solve the problem, only to realize that accounting for air resistance had a miniscule effect on the result.
But there are situations in which air resistance cannot be ignored, such as when calculating the reentry of a spacecraft from orbit. In these cases, what is typically considered a nonessential feature of the equation does significantly impact the results.
As researchers push materials to operate in ever more extreme environments—and design materials on increasingly smaller scales—some features that traditionally did not strongly affect the calculations can no longer be ignored. To account for these additional variables, however, requires the development of new equations that can relate all the contributing factors together.
For example, materials scientists often use grain size as the determining variable when correlating a ceramic’s structure with its properties. The linear intercept technique is commonly used to quantify grain size, but this technique does not consider the morphology and orientation of the grains—variables that can also significantly affect a material’s properties, especially on small scales.
In February 2021, Zhiheng Huang, associate professor of materials physics at Sun Yat-sen University in China, published an open-access paper describing a new framework he developed that can account for grain size and orientation.
Huang used an image classification method proposed by Bruna and Mallat (2013) to construct a set of hierarchical invariants called microStructure Hierarchy Descriptors (µSHDs). These descriptors can be used to quantify the structural hierarchy of a material, and this hierarchy can then be correlated to different materials properties.
In March 2022, Huang and colleagues from other universities in China published a paper showing how they correlated µSHD curves with the mechanical, electrical, and thermal properties of silicon carbide ceramics.
However, “the relationship between hardness and the proposed µSHD has not been dealt with in Huang’s original work,” Huang and colleagues write in a new paper published in May 2023. The new paper aimed to fill this gap, and it did so by proposing a new variable called Asc, or the average of scales.
The scale-related variable Asc is based on the original µSHD concept. It is derived by converting the µSHDs into its original data and then summing the components, eventually arriving at a weighted sum that is Asc.
To calibrate Asc, the authors generated a series of images consisting of fictitious triangular, square, and hexagonal grains of different sizes. After obtaining the corresponding Asc indices from these images, the authors drew two important conclusions.
- Asc is positively linearly correlated with grain size.
- The slope of the fitted line of Asc versus grain size is related to grain morphology.
In other words, “Asc captures not only the scale but also the morphology-related information in the microstructures,” the authors write.
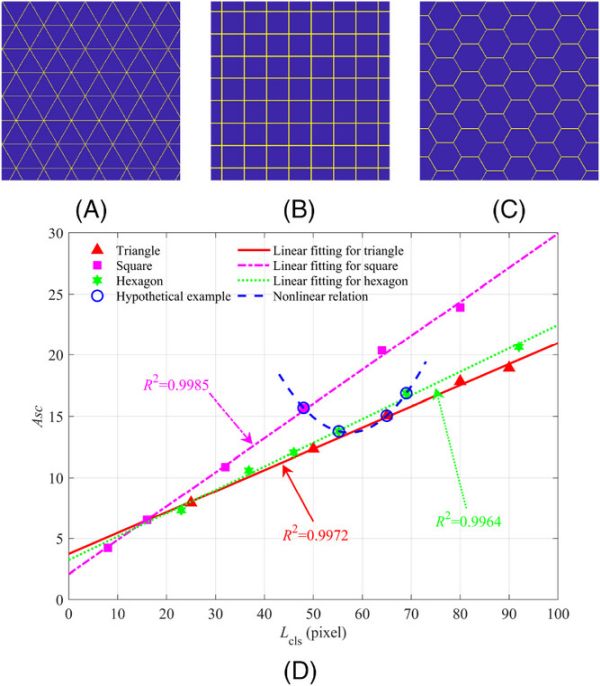
Calibration of the Asc index. A fictitious microstructure containing (A) triangular grains (length scale = 80 pixels), (B) square grains (length scale = 64 pixels), (C) hexagonal grains (length scale = 92 pixels), and (D) scattered data points and fitted lines of Asc versus length scale for the fictitious microstructures analyzed by wavelets with six scales. The circles and the dashed line highlight a hypothetical example. The R2 labels the coefficient of determination of the linear fitting. Credit: Zheng et al., Journal of the American Ceramic Society
When morphology and grain size are considered at the same time, Asc will vary nonlinearly along the length scale, as illustrated by the dashed blue line in the above graph.
To determine the relationship between hardness and Asc, the authors used Vickers hardness as the model hardness index. Excitingly, they discovered that correlations exist between Vickers hardness and Asc in both the direct and inverse Hall–Petch regimes.
The Hall-Petch relation is a quantitative description of how yield strength of a material increases as grain size decreases. However, once grains become smaller than 100 nm, hardness begins to decrease instead, which researchers call the inverse Hall-Petch relation.
Within the direct Hall–Petch regime, which was explored using ZrO2–SiC composite ceramics and a class of high entropy metallic borides, the authors found an inverse correlation between Vickers hardness and Asc. In other words, Vickers hardness increases with a decrease in Asc.
When a ZrO2 ceramic was considered, the authors identified a uniform rule that was valid in both the direct and inverse Hall–Petch regimes. Specifically, that “Asc varies in an opposite trend as the HV [Vickers hardness] varies with grain size d,” the authors write.
The authors conclude that further consistent experimental data is needed to establish the general applicability of the relationship between the Vickers hardness and Asc.
The paper, published in Journal of the American Ceramic Society, is “A uniform rule between hardness and structure hierarchy of ceramics in both direct and inverse Hall–Petch regimes” (DOI: 10.1111/jace.19224).
Author
Lisa McDonald
CTT Categories
- Basic Science