[Image above] Ordered and disordered materials transport heat quite differently based on their contrasting atomic structures. Two formulas now are capable of describing thermal transport in both. Credit: the glass-blower, Flickr (CC BY 2.0)
One thing I appreciate deeply about math is that you can arrive at the same answer in multiple ways. My favorite example is when I successfully argued back points on my Calculus 3 test after convincing the professor I solved the problem with an alternative method used in the book rather than the method he taught in class.
Neither method was inherently more “right” or “wrong” than the other (both generated the same answer, after all). But the two methods demonstrated how your understanding of a problem is shaped based on the way in which you solve it. In that sense, having multiple methods by which to solve a single problem gives you an expanded comprehension of the issue at hand.
Which is why a new equation for modeling heat transport in both crystals and glasses provides such a nice complement to the formula I wrote about in June.
At that time, I discussed how researchers at the Swiss Federal Institute of Technology Lausanne–EPFL and the University of Rome Sapienza derived a general formula of thermal transport that described equally well both ordered and disordered materials, as well as everything in between. They derived the equation from the Wigner phase space formulation of quantum mechanics.
Early this week, a new open-access paper was published in Nature Communications that referred to this study in its conclusion. “While this paper was being written we learnt that conclusions similar to ours were reached by Simoncelli et al., following a different approach based on a generalization of the BTE [Boltzmann transport equation],” the researchers write.
The researchers of the new study—Leyla Isaeva (postdoc) and Stefano Baroni (professor) from the International School for Advanced Studies (SISSA) in Italy, and Giuseppe Barbalinardo (Ph.D. candidate) and Davide Donadio (professor) at the University of California, Davis—also created a novel approach to model heat transport in crystals and glasses. However, instead of deriving their formula from the Wigner phase space formulation, they derived their formula from the Green-Kubo (GK) theory of linear response.
The GK theory of linear response says that a material’s thermal conductivity can be expressed in terms of time correlations of the heat current. “Far from melting, the energy flux and the lattice Hamiltonian of a solid, both crystalline and amorphous, can be expressed as power series in the atomic displacements,” the researchers write in the paper. Thus, “Eq. (1) can be evaluated in terms of Gaussian integrals using standard field-theoretical techniques.”
The researchers combined the GK theory and a quasi-harmonic description of lattice vibrations to create a compact expression for thermal conductivity. The expression “unifies the BTE approach in the single-mode relaxation-time approximation (RTA) for crystals and a generalization of the Allen-Feldman (AF) model for disordered system that explicitly and naturally accounts for normal-mode lifetimes,” they explain.
To verify their formula—dubbed the quasi-harmonic Green Kubo (QHGK) approximation—the researchers compared its predictions with ones derived by equilibrium molecular dynamics simulations for crystalline and amorphous silicon and BTE computations for crystalline silicon.
Based on these comparisons, the researchers conclude, “QHGK provides a significant improvement in generality over the Allen-Feldman model for disordered systems and is analytically proven to be equivalent to BTE for periodic systems.”
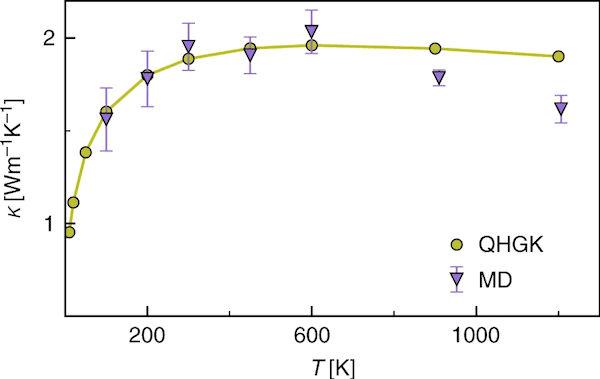
Comparison between thermal conductivity of amorphous silicon computed for a 1728-atom supercell by classical Green–Kubo theory of linear response using either the new QHGK approach (green) or equilibrium molecular dynamics (purple). Credit: Isaeva et al., Nature Communications (CC BY 4.0)
With now two formulas available for modeling heat transport in crystals and glass, researchers looking to develop materials that are both crystal-like and glass-like for use as thermoelectrics are better prepared than ever before.
The open-access paper, published in Nature Communications, is “Modeling heat transport in crystals and glasses from a unified lattice-dynamical approach” (DOI: 10.1038/s41467-019-11572-4).
Author
Lisa McDonald
CTT Categories
- Glass
- Thermal management